Per calcolare correttamente un ponte termico con metodo FEM è necessario analizzare la tipologia di discontinuità, caratterizzarne la regione di calcolo e, quindi, introdurre tutti gli elementi che possono influenzarne l'andamento delle linee di flusso.
Lo strumento più utile per poter effettuare correttamente il tutto è il wizard. In questo modo, infatti, sarà il programma a recuperare e impostare in automatico tutte le informazioni necessarie al calcolo. Di seguito verranno trattati alcuni casi notevoli, al fine di comprendere l'inserimento dati e acquisire gli strumenti per poter introdurre delle personalizzazioni e delle modifiche ai modelli o addirittura costruire modelli di ponti termici del tutto nuovi.
Wizard - Angolo sporgente
Sia una parete di spessore pari a 30 cm. Si vuole calcolare il ponte termico relativo all'angolo sporgente in cui entrambi i lati sono costituiti dalla stessa parete. Una volta definita la stratigrafia e importata nel modulo di calcolo del ponte termico si ha:
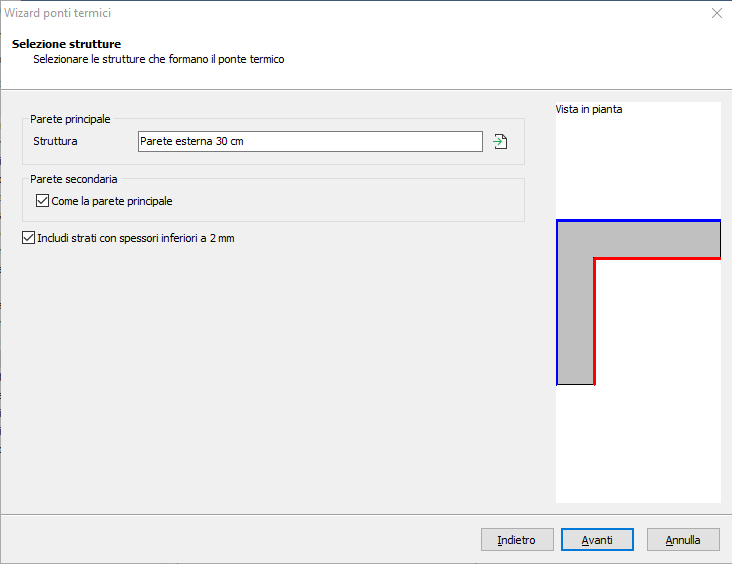
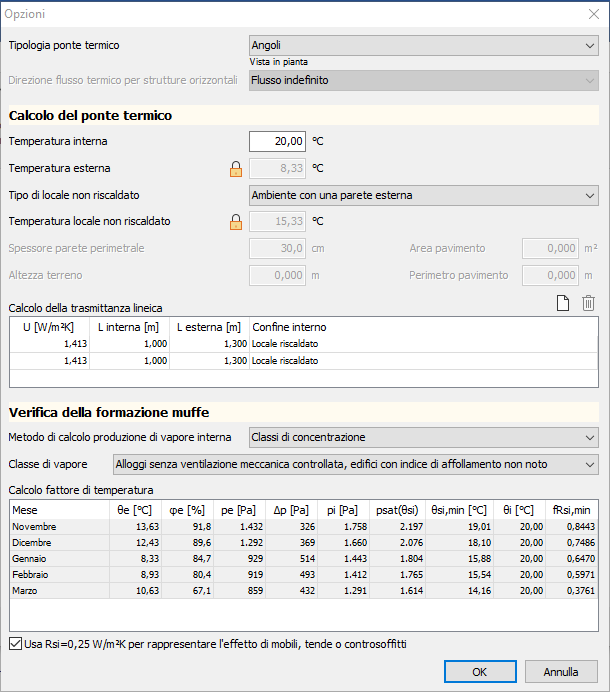
Premendo sul pulsante "Opzioni" si potranno osservare le impostazioni di calcolo compilate in automatico dal programma. La parte più importante è rappresentata dalla tabella "Calcolo della trasmittanza lineica"
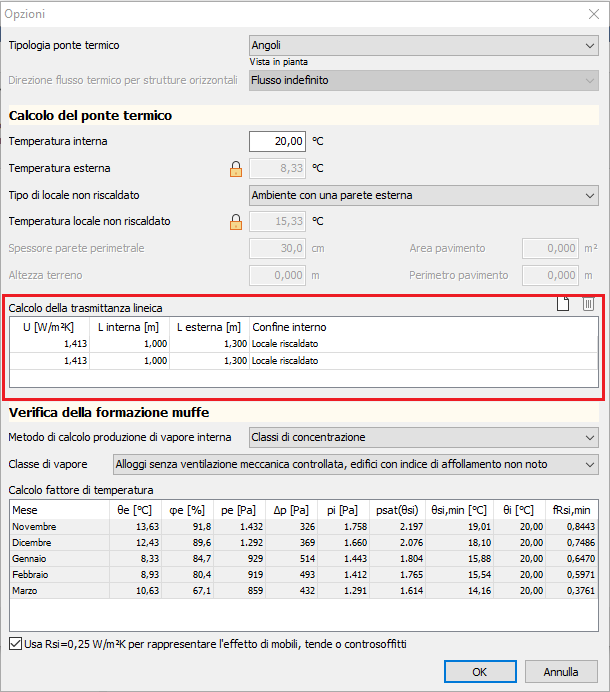
In questa tabella vengono riportate le caratteristiche termiche e geometriche delle strutture che costituiscono la discontinuità. In questo caso vediamo che le righe sono 2, ovvero pari al numero delle strutture che generano il ponte termico, in altre parole le due pareti. La tabella seguente illustra il significato delle varie colonne.
| U | Qui viene semplicemente riportata la trasmittanza della struttura a cui si riferisce la riga |
| L interna | Rappresenta la lunghezza della struttura misurata dal lato interno della discontinuità stessa. Per determinare questa lunghezza occorre riferirsi a precise specifiche fornite dalla UNI EN ISO 10211. Tale lunghezza, infatti, deve essere pari 3 volte lo spessore della struttura e al minimo 1 m. |
| L esterna | Rappresenta la lunghezza della struttura misurata sul lato esterno. Ovviamente per determinare questa lunghezza è necessario fissare prima quella interna. |
| Confine interno | Permette di definire l'esposizione della struttura dal lato interno |
Vediamo di ricavare manualmente i valori già inseriti nelle varie colonne, sulla base di quanto specificato nella tabella precedente, in modo da comprenderne meglio il significato.
La parete utilizzata nel calcolo è la seguente:
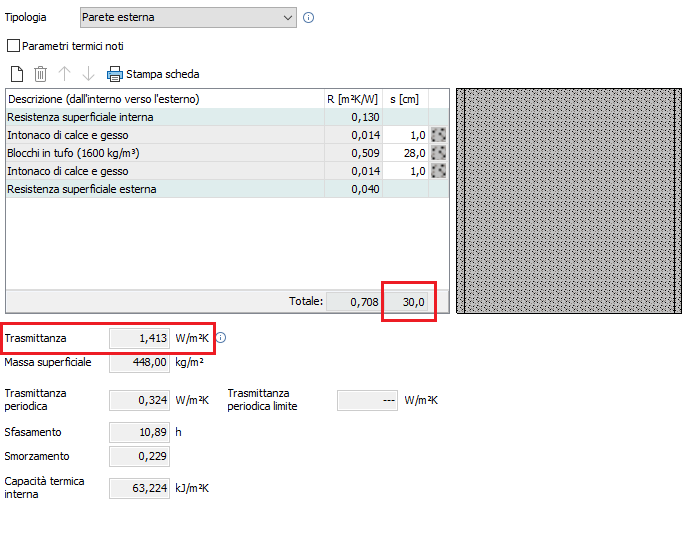
La trasmittanza U si può immediatamente leggere dalla finestra precedente.
Per quanto riguarda la L Interna, questa si riferisce alla lunghezza evidenziata in giallo di seguito:
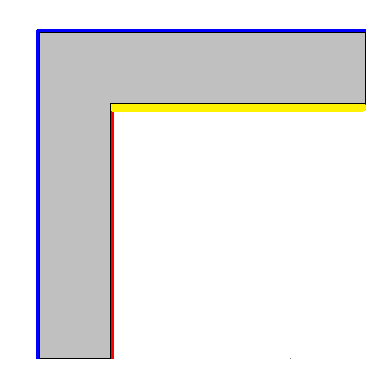
Essa deve essere pari a 3 volte lo spessore della parete, essendo quest'ultimo pari a 30 cm, si avrà:
3x0.3 = 0.9 m
Poiché il valore minimo fissato dalla norma è pari a 1 m, allora si considererà quest'ultimo.
Per quanto riguarda la L esterna, questa è la lunghezza evidenziata in giallo nella figura successiva:
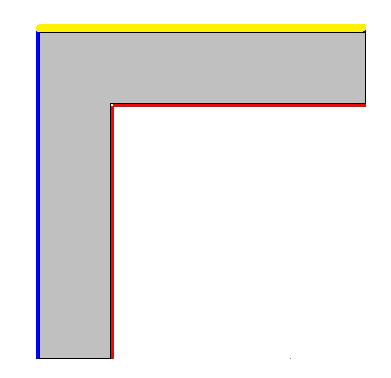
è facile dedurre che questa lunghezza è data da L interna + lo spessore della seconda parete. Si ha, quindi:
L esterna = 1+0.3 = 1.3 m
Sulla base di queste considerazioni sarà facile personalizzare le tabelle quando necessario.
Vediamo cosa succede quando si introduce nel modello, un pilastro da 40 cm, quindi, più spesso delle pareti:
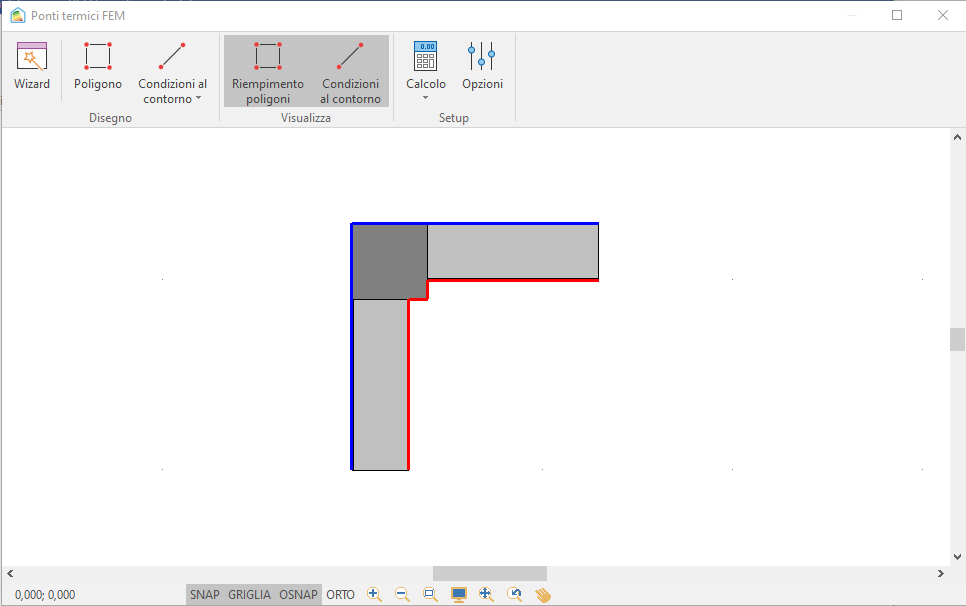
Osservando le opzioni di calcolo, si nota che la tabella delle trasmittanze è rimasta invariata:
Questo è corretto, in quanto le strutture che determinano la discontinuità sono rimaste le stesse e il pilastro è solo un oggetto che altera le linee di flusso.
Ciò vuole dire che non sempre è necessario modificare la tabella delle trasmittanze o introdurre righe per ogni elemento presente nel ponte termico. In generale, anzi, le righe saranno sempre due, eccetto nei casi di pavimenti su terreno o ponti termici composti (ovvero formati da più ponti termici insieme) nei quali si potranno avere tre righe.
Wizard - Balcone
Un altro esempio molto utile è quello del ponte termico balcone. Sia il caso di un semplice balcone con parete isolata all'esterno, balcone non isolato e trave:
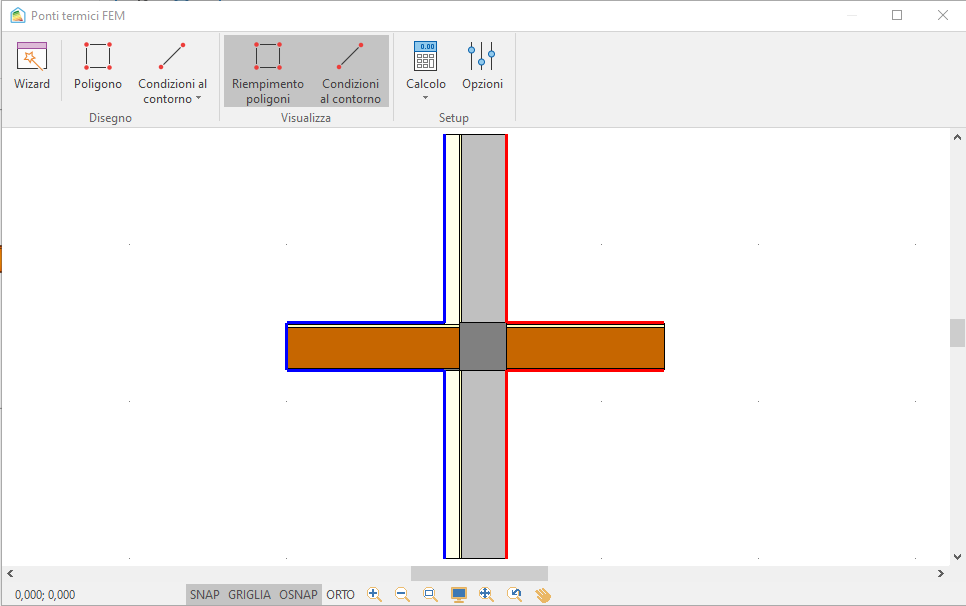
Le caratteristiche delle strutture coinvolte sono:
| Spessore (cm) | Trasmittanza (W/mqK) | |
| Parete esterna | 40 cm | 0.268 |
| Solaio interno | 30 cm | 1.527 |
| Balcone | 30 cm | 1.653 |
Vediamo come il programma ha costruito le opzioni di calcolo:
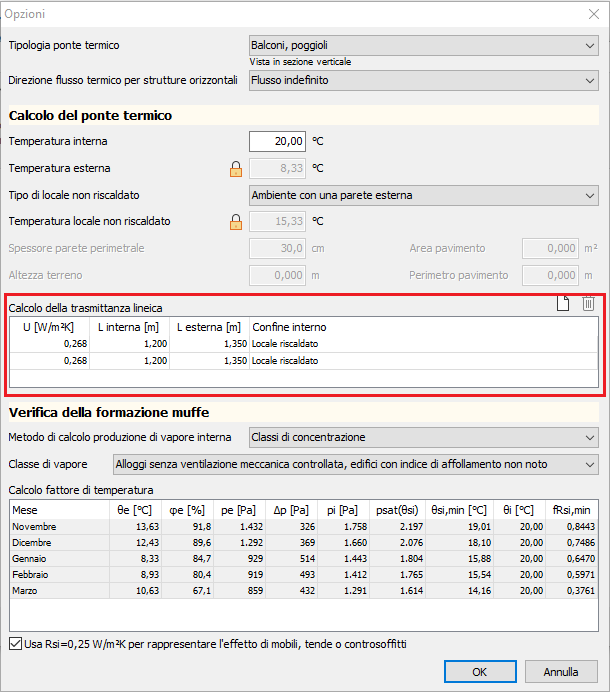
Osserviamo ancora una volta solo due righe che rappresentano le porzioni di parete superiore e inferiore. Sono queste, infatti, le strutture disperdenti che determinano discontinuità vera e propria.
La U, infatti, è quella della parete.
La Lunghezza interna è quella evidenziata in giallo nell'immagine successiva ed è calcolata come da norma, ovvero 3 volte lo spessore della parete (3x0.40 m = 1.2 m).
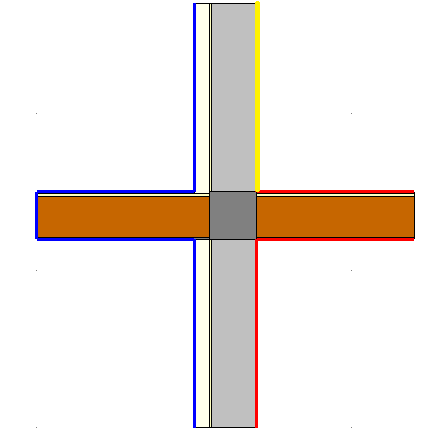
La lunghezza esterna, invece, è data dalla lunghezza interna alla quale va aggiunto metà spessore del solaio interno in quanto non disperdente. Pertanto si ha:
L esterna = 1.2 + (1/2 * 0.3 ) = 1.35 m.
Le due righe sono identiche perché identiche sono le pareti. Non vi sono, inoltre, riferimenti al solaio, al balcone e alla trave che sono elementi esterni o non disperdenti.
Lanciando il calcolo si ottengono i seguenti risultati:
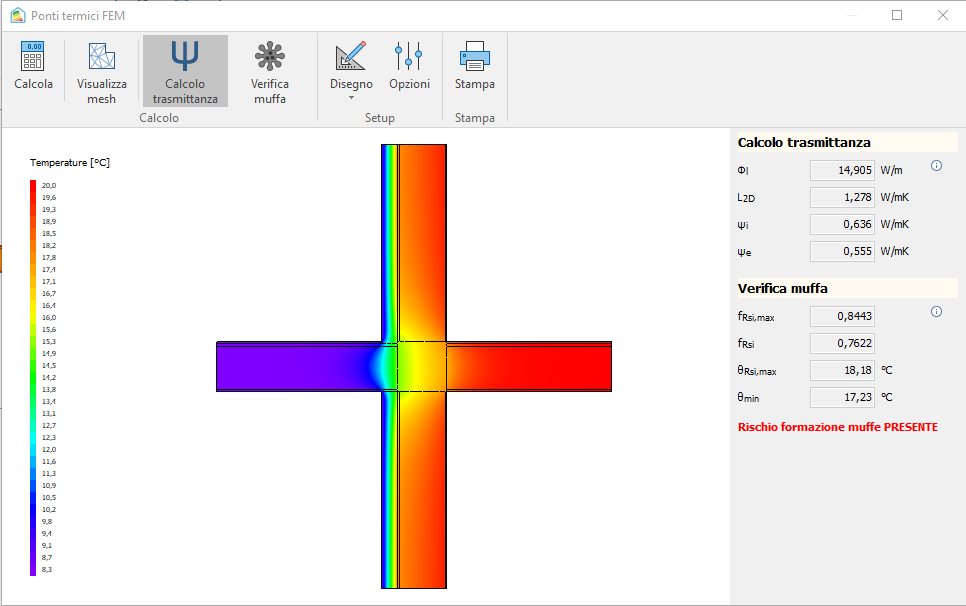
Si vuole, adesso, provare a ridurre l'incidenza del ponte termico isolando il balcone all'intradosso. Questo si può fare in due modi: isolando la struttura nella definizione della stratigrafia, e quindi rieseguendo il wizard, oppure manualmente disegnando lo strato di isolamento e successivamente aggiustando le condizioni al contorno. Come spiegato sopra, non sarà necessario agire sulle opzioni di calcolo in quanto il balcone è una struttura non disperdente. Si ottiene la situazione seguente:
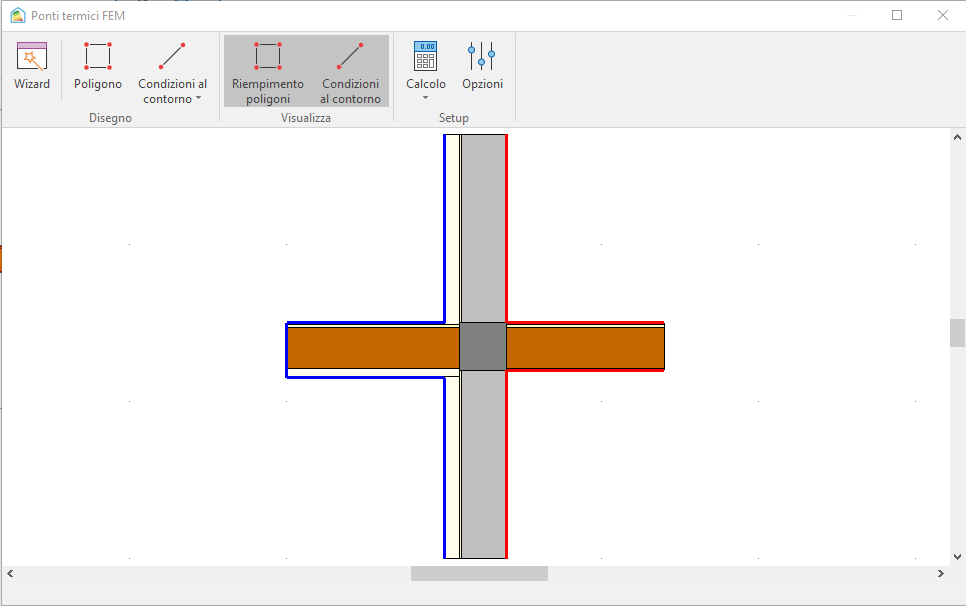
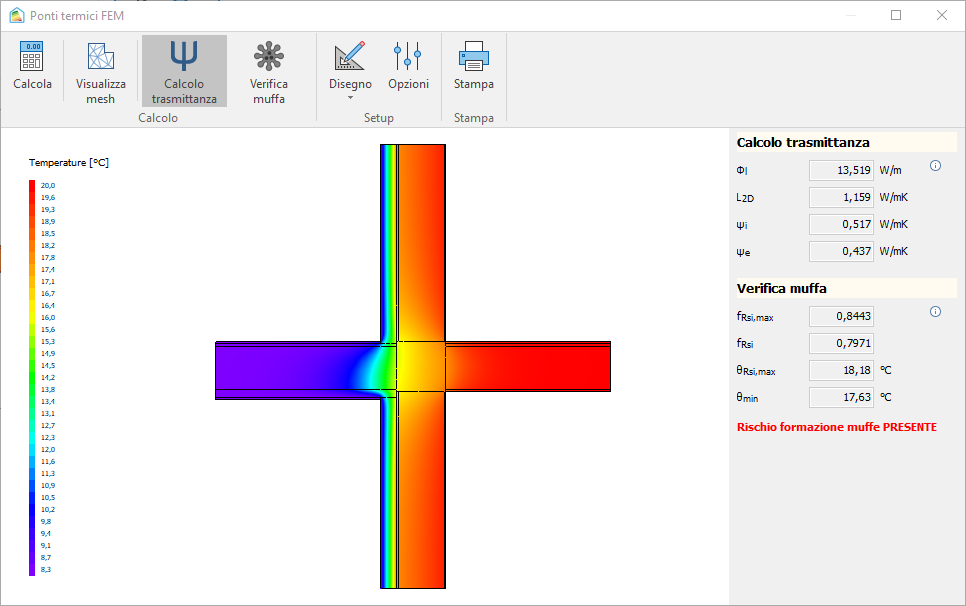
Con uno strato di isolamento di 5 cm, la trasmittanza lineica esterna si è ridotta del 21.3%.
Esempio di personalizzazione di ponte termico
Si vuole, adesso, gestire un caso più complesso costituito dal ponte termico generato da un terrazzo, che costituisce la copertura del piano terra, sulla parete esterna del piano primo. In altre parole la discontinuità evidenziata nella successiva immagine:
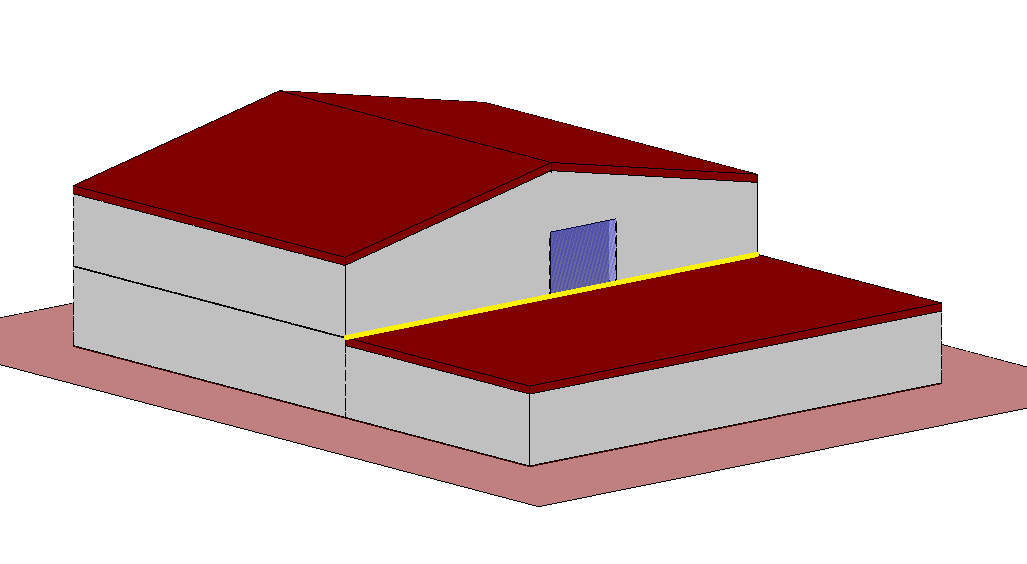
In corrispondenza della parete esterna, al piano terra, si trova una parete interna che ovviamente non è disperdente, separando ambienti riscaldati.
Le strutture coinvolte sono:
| Spessore [cm] | Trasmittanza [W/mqK] | |
| Parete esterna | 30 | 1.413 |
| Copertura | 30 | 1.870 |
| Parete interna | 30 | 1.254 |
Il caso che più si avvicina alla situazione in esame è senza dubbio quello della copertura. Vediamo come utilizzarlo. Impostando la copertura tramite wizard e introducendo un'estensione superiore della parete di 100 cm si ottiene la situazione seguente:
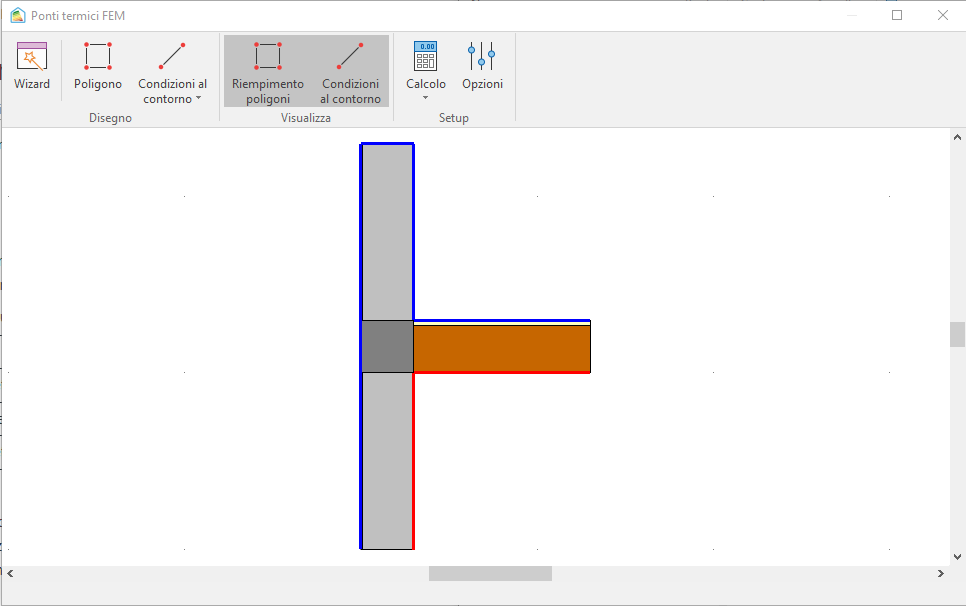
Nella situazione reale, invece, sul lato sinistro della parete si ha l'ambiente interno, mentre l'esterno si trova solo nel quadrante in alto a destra. Il primo passo da fare, quindi, è quello di cambiare la condizione al contorno sinistra, ottenendo:
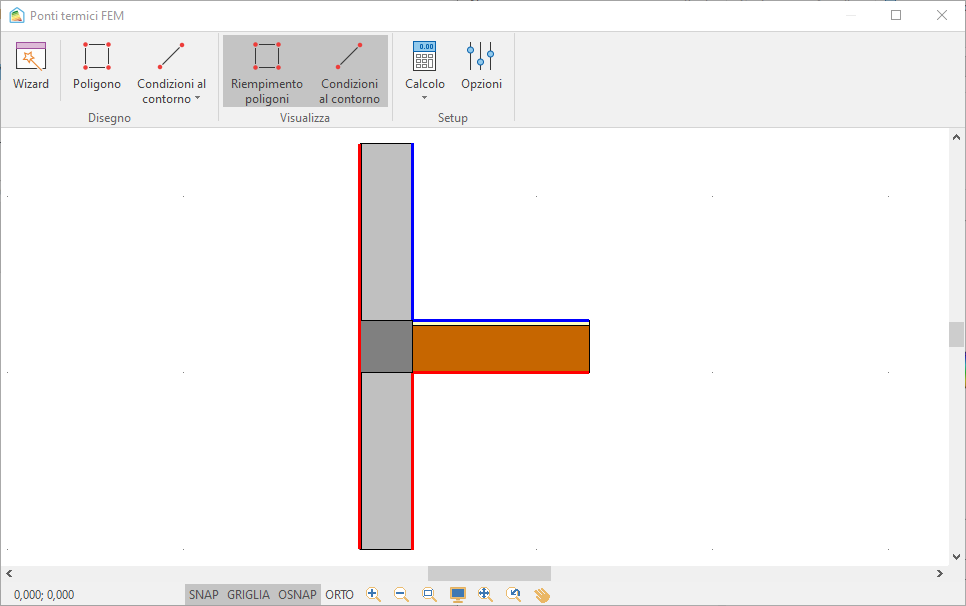
Osservando il ponte termico si evince che la discontinuità vera e propria è rappresentata solo dalla parete esterna superiore e dalla copertura, essendo la parete inferiore non disperdente. In sintesi le lunghezze interne ed esterne che costituiscono la discontinuità sono quelle evidenziate di seguito in giallo (interno) e viola (esterno):
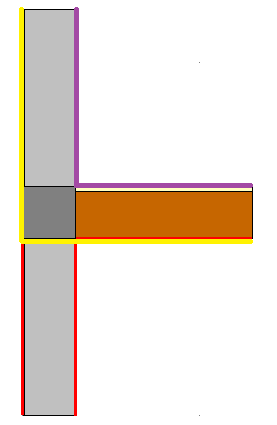
Anche in questo caso, il ponte termico sarà costituito solo da due righe.
Per quanto riguarda la parete, la lunghezza esterna, in questo caso, è inferiore rispetto a quella interna, come si evince facilmente dal disegno. Ponendo la lunghezza esterna pari a 3 volte spessore di ha:
3x0.3 = 0.9 m
quindi, al minimo 1 m.
La lunghezza interna, invece, sarà pari alla lunghezza esterna alla quale va aggiunto lo spessore della copertura. Quindi:
1+0.3 = 1.3 m
Per la copertura valgono considerazioni del tutto simili a quelle della parete. Le opzioni del ponte termico, quindi, vanno modificate come mostrato nella successiva immagine:
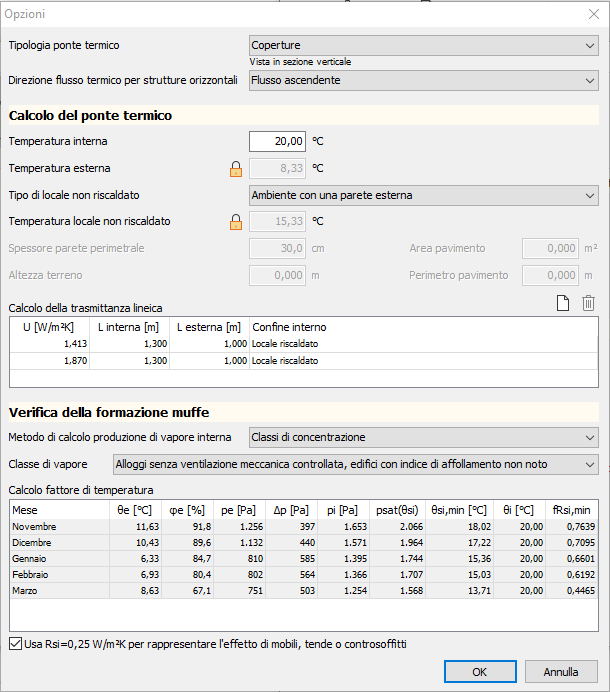
Il risultato del ponte termico è il seguente:
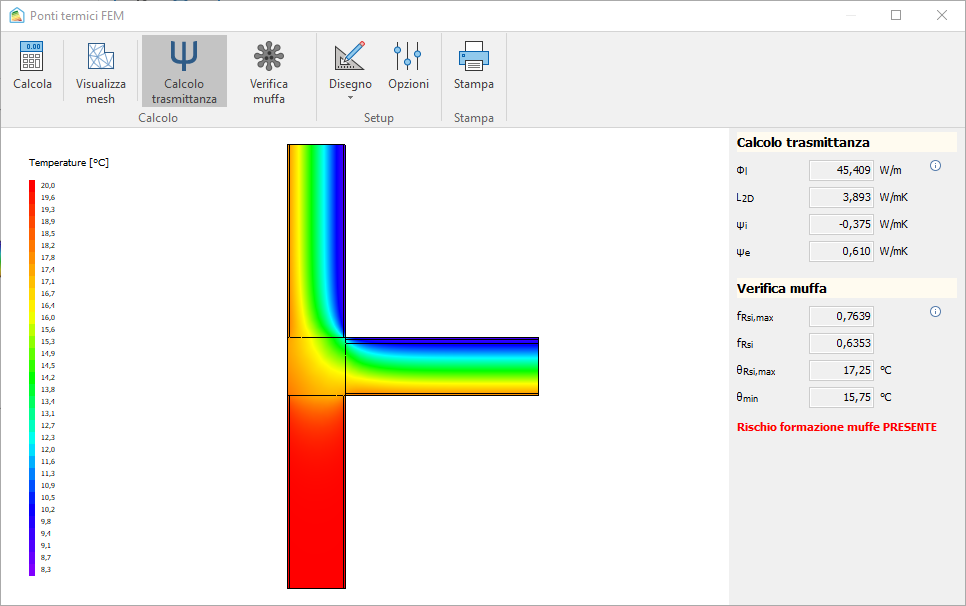
Considerazioni finali
La modellazione di un ponte termico, come visto, richiede di valutare attentamente la discontinuità in modo da adeguare, se necessario, le condizioni di calcolo. Lo strumento ideale per gestire ogni ponte termico è il wizard, pertanto, è sempre preferibile generare la casistica usando questo strumento e, successivamente, introdurre le variazioni che si desiderano graficamente. La necessità di agire sulle opzioni, infine, nasce tutte le volte in cui le strutture che determinano la discontinuità vengono modificate in modo sostanziale oppure se si cambiano le condizioni al contorno.
Se hai bisogno di ulteriore assistenza